When we observe a TV or a laptop screen, a kite, the cover of a book, a ruler, and even a tennis court, we conclude that we see four sided, closed shapes that are four sided in different ways.These shapes are known as quadrilaterals.

Quadrilateral Definition

Ideally, a quadrilateral is a four-sided polygon (In geometry, a polygon can be defined as a flat, closed shape with straight sides) that has four vertices (typically means a corner or a point where lines meet).

Quadrilateral Meaning

The word quadrilateral’s roots can be traced to the Latin words quadri and latus, which mean ‘four’ and ‘side’ respectively. With reference to a triangle, a quadrilateral is also known as a quadrangle, with the prefix ‘quad’ indicating a four sided figure with four angles in it.

Properties of a quadrilateral :

To understand the properties of a quadrilateral, refer to one of the three diagrams of □PQRS given below (Preferably the simple quadrilaterals for better understanding).

• A quadrilateral with the vertices P,Q, R and S is denoted as □PQRS.

• A quadrilateral has two pairs of opposite sides. In □PQRS, QR is opposite to PS and QP is opposite to RS. Every side has just one opposite side.

• A quadrilateral has four pairs of adjacent sides. In □PQRS, PQ and QR, QR and RS, RS and SP, SP and PQ are all pairs of adjacent sides. Every side has two adjacent sides.

• The diagonals of a quadrilateral refer to the line segments connecting two opposite vertices. Every quadrilateral has two diagonals. In □PQRS, PR and QS are the diagonals.

• A quadrilateral has two pairs of opposite angles. In □PQRS, ∠PQR is opposite to ∠ PSR and ∠ QPS is opposite to ∠ QRS . Every angle has just one opposite angle.

• A quadrilateral has four pairs of adjacent angles. In □PQRS, ∠PQR and ∠QRS, ∠QRS and ∠RSP, ∠RSP and ∠SPQ, ∠SPQ and ∠PQR are all pairs of adjacent angles. Every angle has two adjacent angles.

Types of Quadrilaterals

Simple Quadrilaterals

• Convex Quadrilaterals

Parallelogram and its features:

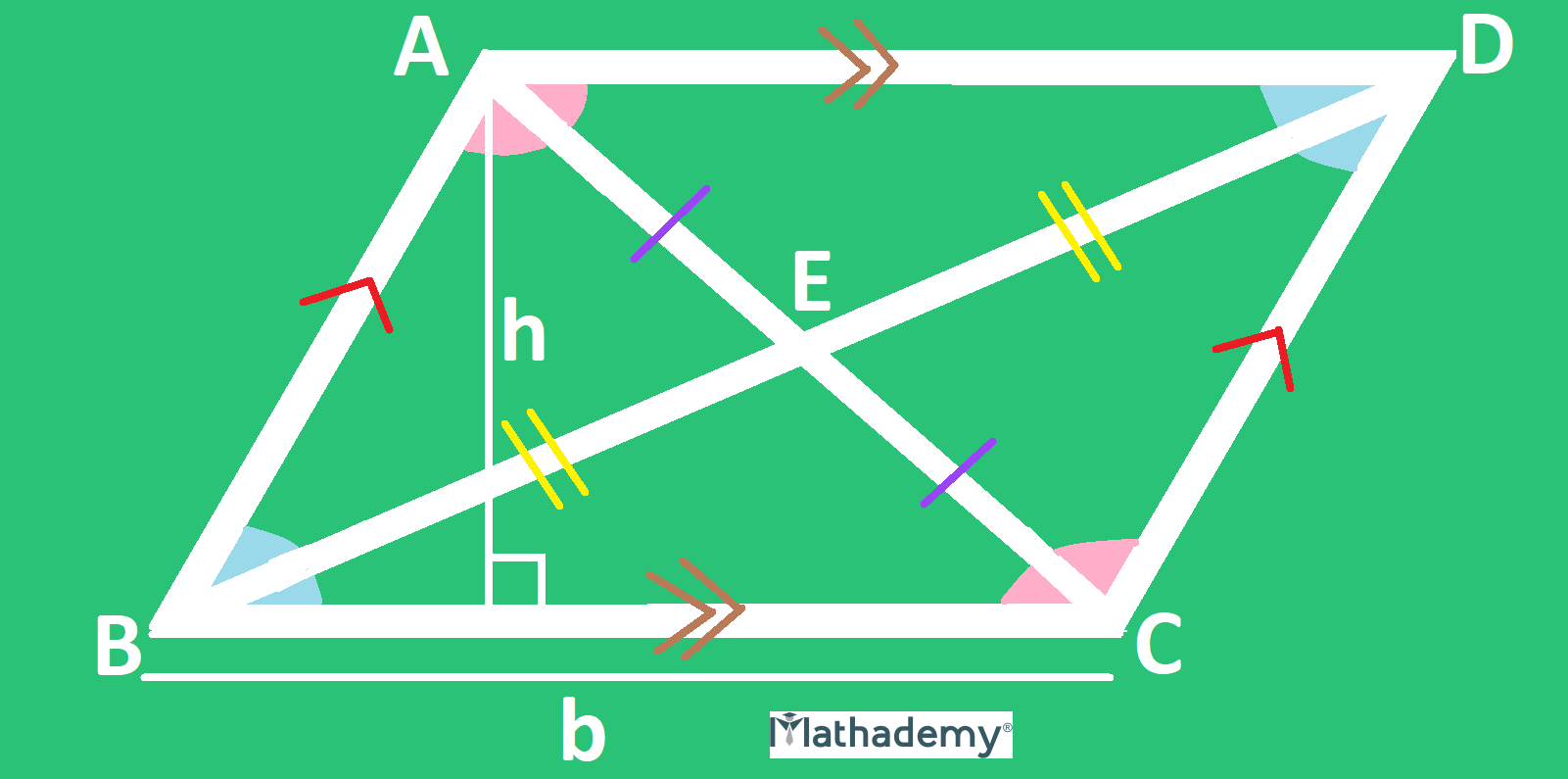
• There are two pairs of parallel sides.

• The opposite sides are equal.

• The opposite angles are equal.

• The adjacent angles are supplementary (their sum adds up to 180°).

The diagonals bisect each other.

• Every diagonal divides the parallelogram into two equal triangles.

The perimeter of a parallelogram ABCD = sum of the lengths of its four sides = AB +BC + CD + AD

The area of a parallelogram ABCD = base x height = b x h

Quadrilaterals Example:

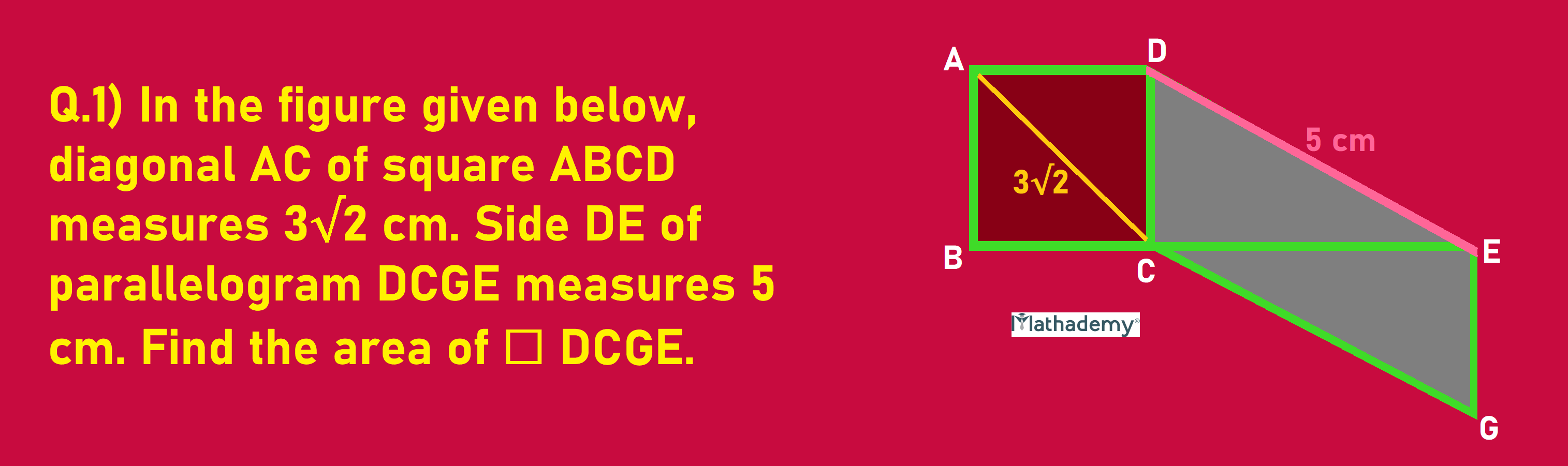
Solution:

We know that every angle of a square is a right angle and the four sides are equal.

∴DC = AD

∴ By Pythagoras’ theorem, AD ² + DC² =AC²

∴DC ²+DC ² = AC ²

∴ 2 DC ² = AC ²

∴2 DC ² =(3√2) ²

∴2 DC ² = 3 x 3 x √2 x √2

∴2 DC ² = 9 x 2

∴DC ² = 9

∴ DC = √9

∴ DC = 3

We know that ∠ DCB = 90° (Measure of all angles of a square are 90°)

∴ ∠ DCE + ∠ DCB = 180° (Angles in a linear pair are supplementary)

∴ ∠ DCE = 90°

∴ By Pythagoras’ theorem, DC² + CE² = DE²

∴3² + CE² = 5²

∴ 9 + CE² = 25

∴ CE² = 25 – 9

∴ CE² = 16

∴ CE = ±√ 16

∴ CE = ± 4

Since the length of anything cannot be a negative number, CE = 4 cm

We know that the area of △DCE = (½) x CE x DE

= (½) x 4 x 3

= 2 x 3

= 6

△DCE = 6 cm ²

We know every diagonal divides the parallelogram into two equal triangles.

∴ △DCE =△CEG

∴ Area of □DCGE = △DCE + △CEG

= 6 + 6

= 12

Hence area of parallelogram DCGE = 12 cm²

Rhombus and its features:

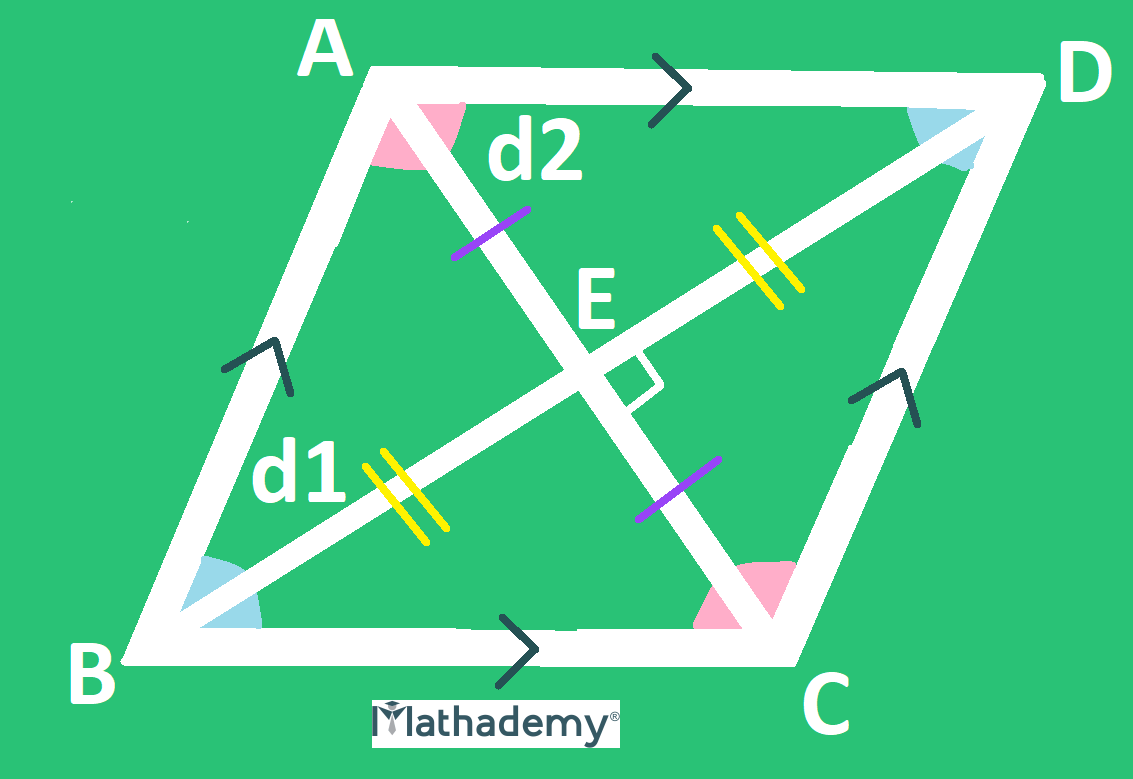
• There are two pairs of parallel sides.

• The opposite angles are equal.

• The adjacent angles are supplementary (their sum adds up to 180°).

• The diagonals bisect each other.

• Every diagonal divides the rhombus into two equal triangles.

• All the four sides are equal.

• The diagonals are perpendicular to each other.

The perimeter of a rhombus ABCD = sum of the lengths of its four sides = AB +BC + CD + AD

The area of a rhombus ABCD = (½) x length of first diagonal x length of second diagonal =(½) x d1 x d2

Quadrilaterals Example:

Solution:

We know that the diagonals of a rhombus are perpendicular bisectors of each other.

∴ BP = PE = (½) BE = 20/2 = 10 cm

∴AP = PC = (½) AC = 10/2 = 5 cm

The area of rhombus BAEC = d1 x d2/ 2

= AC x BE/2

= 10 x 20/2

= 100 cm sq

We know that the breadth of rectangle PEGK is formed by PE = 10 cm

We know that the length of rectangle PEGK is formed by PK = PC + CK

= 5 + CK

The area of rectangle PEGK is twice the area of rhombus BAEC

∴ 2x100 = length x breadth

∴200 = (5 + CK)10

∴ 200 = 50 + 10CK

∴ 200 – 50 = 10CK

∴150 = 10CK

∴150/10 = CK

∴ 15 cm = CK

We know that length of rectangle PEGK = PK = PC +CK =5 + 15 = 20 cm

Rectangle and its features:

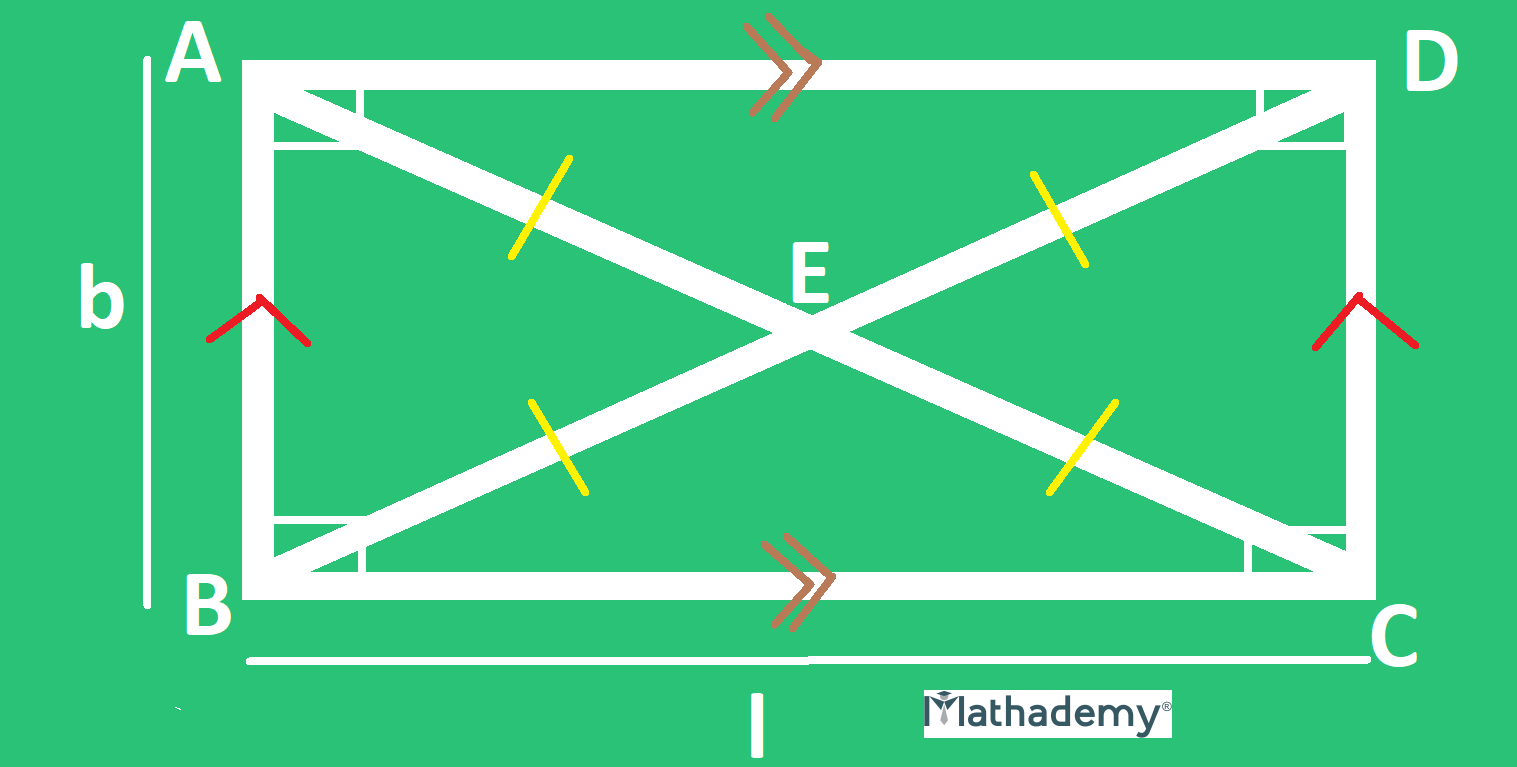
• There are two pairs of parallel sides.

• The opposite angles are equal.

• The adjacent angles are supplementary (their sum adds up to 180°).

• The diagonals bisect each other.

• Every diagonal divides the rectangle into two equal triangles.

• The diagonals are equal in length.

• All the angles are right angles ( each angle is 90°).

The perimeter of a rectangle ABCD = sum of the lengths of its four sides = AB +BC + CD + AD

The area of a rectangle ABCD = length x breadth = l x b

Square and its features:

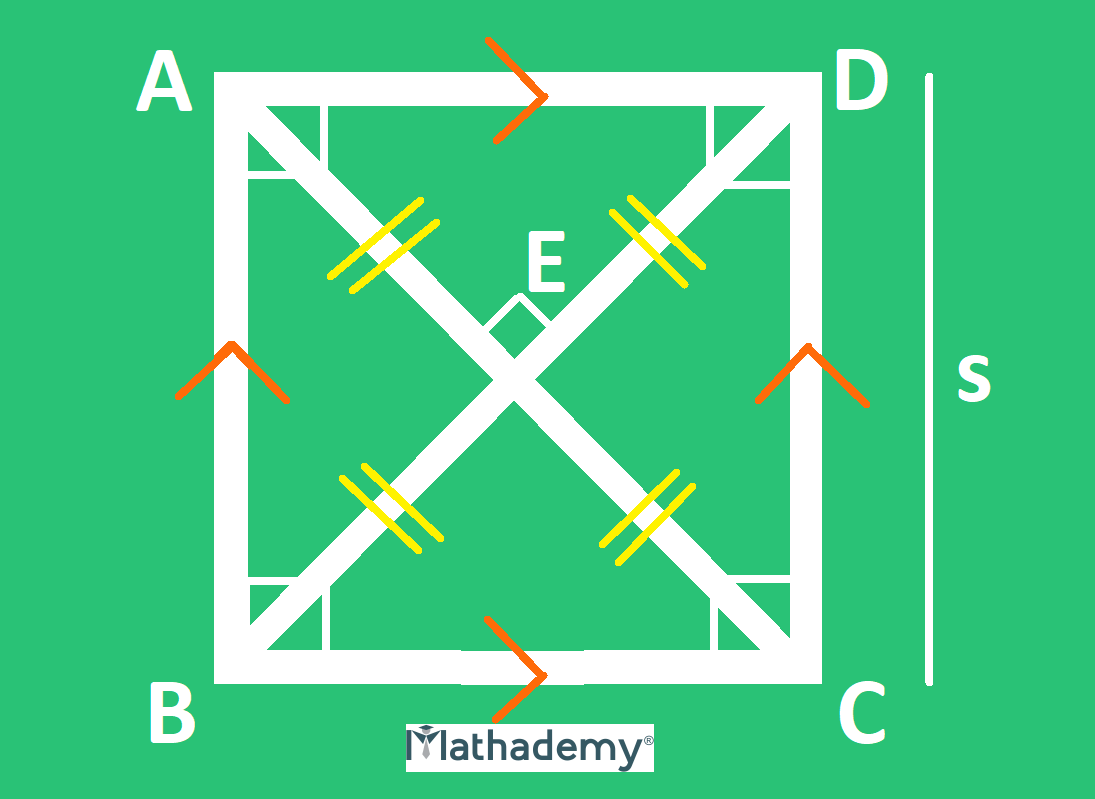
• There are two pairs of parallel sides.

• The adjacent angles are supplementary (their sum adds up to 180°).

• The diagonals bisect each other. The measure of any diagonal of a square is √2 times the measure of the side.

• Every diagonal divides the square into two equal triangles.

• All the four sides are equal.

• The diagonals are perpendicular to each other.

• The diagonals are equal in length.

• All the angles are right angles ( each angle is 90°)

The perimeter of a square ABCD = sum of the lengths of its four sides = AB +BC + CD + AD units

The area of a square ABCD = side x side = side² = s ²

Quadrilaterals Example:

Solution:

We know that □LMNO is a square

∴∠LMN = ∠ONM = 90°

We know that △MPN is an equilateral triangle.

∴ ∠LMN = ∠ ONM = ∠LMP + ∠PMN = ∠ONP + ∠PNM = 90

∴ ∠ LMP = ∠ONP = ∠LMN - ∠PMN = ONM - ∠PNM = 90 - 60 = 30° (Measure of all angles of an equilateral triangle is 60°)

We know that side MN of square LMNO is also the side of equilateral triangle MPN.

∴ MN = PM = PN = LM = ON

∴△ LMP and △ONP are isosceles triangles where LM = MP and ON = OP

∴ ∠ MLP = ∠ MPL = ∠NPO = ∠ NOP

We know that the sum of all the angles of a triangle is 180°

Since ∠ LMP = ∠ONP = 30°,

∠ MLP + ∠ MPL = ∠NPO +∠ NOP = 180 - 30 = 150°

We know that ∠ MLP = ∠ MPL = ∠NPO = ∠ NOP

∠ MLP + ∠ MLP = 150° and ∠NOP + ∠NOP = 150°

2∠ MLP = 150 and 2 ∠NOP = 150

∠ MLP = 150/2 and ∠NOP = 150/2

∠ MLP = 75° and ∠NOP = 75°

Since ∠MNO and ∠NOL = 90°

∠PLO = ∠POL = 90 – 75 = 15°

We know that in △LPO, ∠PLO + ∠POL + ∠LPO = 180°

∴ 15 + 15 + ∠LPO = 180

∴ 30 + ∠LPO = 180

∴ ∠LPO = 180 – 30 = 150°

Hence, the measure of ∠LPO = 150°

Trapezium and its features:

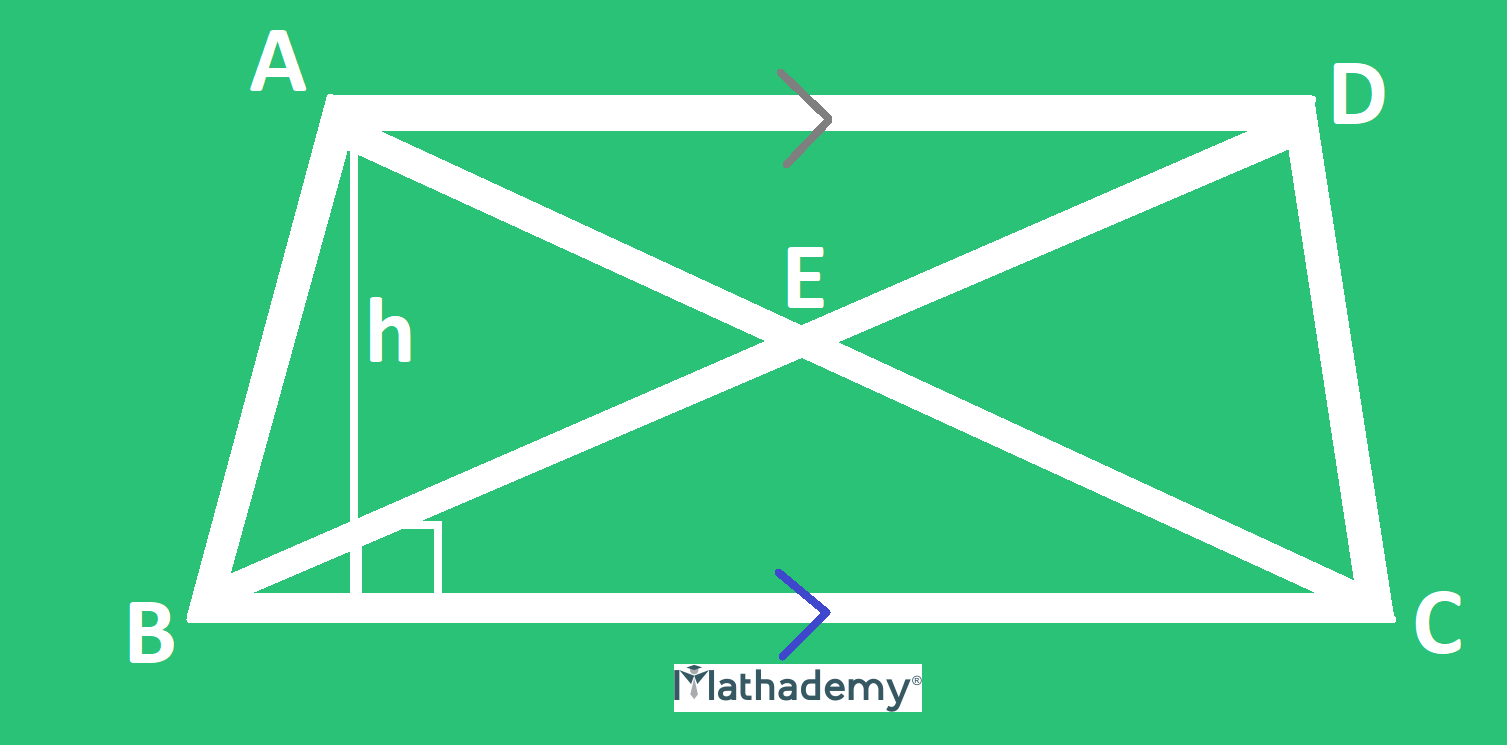
• There is at least one pair of parallel sides. The other two sides may or may not be parallel to each other. In case that the pair of non parallel sides is having the same length, the trapezium is termed as isosceles trapezium.

The perimeter of a trapezium ABCD = sum of the lengths of its four sides = AB +BC + CD + AD

The area of a trapezium ABCD =(½) x sum of parallel sides x height

Quadrilaterals Example:

Q.4)The area of a trapezium is 75 cm sq. If the height of the trapezium is 5 cm and if the lengths of its parallel sides y cm and y + 10 cm, find the measure of the lengths of its parallel sides in numerical terms.

Solution:

We know that the area of a trapezium = sum of parallel sides x height/2

∴ 75 = (y + y +10) (5)/ 2

∴75 = (2y +10) (5)/2

∴75 x 2 = (2y + 10) (5)

∴150 = 10y + 50

∴150 – 50 = 10y

∴ 100 = 10y

∴100/10 = y

∴ 10 = y

∴ y +10 = 10 + 10 = 20

We know that the length of the two parallel sides are y and y + 10.

Hence, the lengths of the two parallel sides of the trapezium are 10 cm and 20 cm.

Kite and its features:

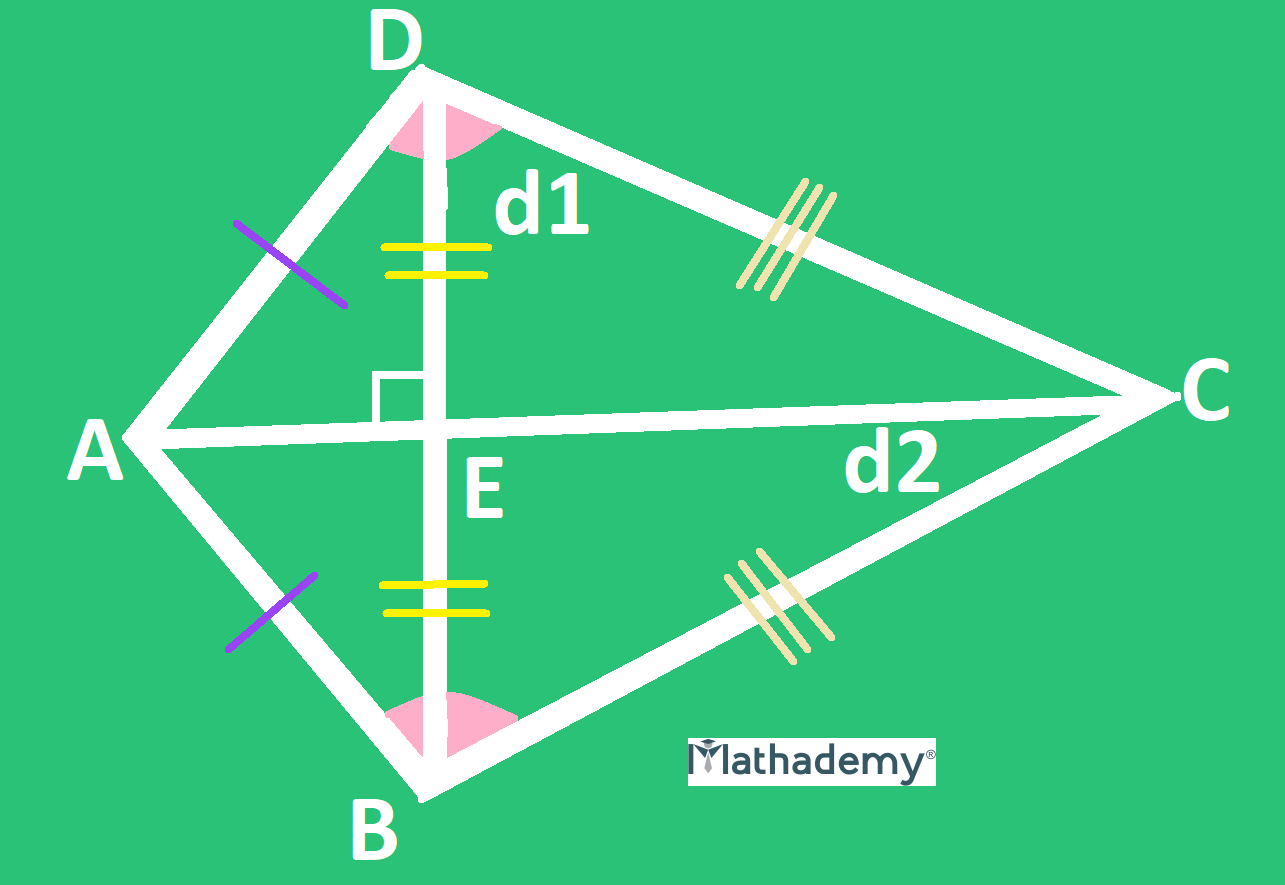
• There is at least one pair of equal adjacent sides.

• The diagonals are perpendicular to each other.

• There is at least one pair of equal opposite angles

• There is at least one diagonal which bisects the other diagonal.

The perimeter of a kite ABCD = sum of the lengths of its four sides = AB +BC + CD + AD

The area of a kite ABCD = (½) length of first diagonal x length of second diagonal = (½) x d1 x d2

Irregular quadrilateral and its features:

• None of the four sides are parallel to each other

The perimeter of a quadrilateral ABCD = sum of the lengths of its four sides = AB +BC + CD + AD units

The area of quadrilateral ABCD = (½) x diagonal x sum of length of perpendiculars drawn to the same diagonal

Quadrilaterals Example:

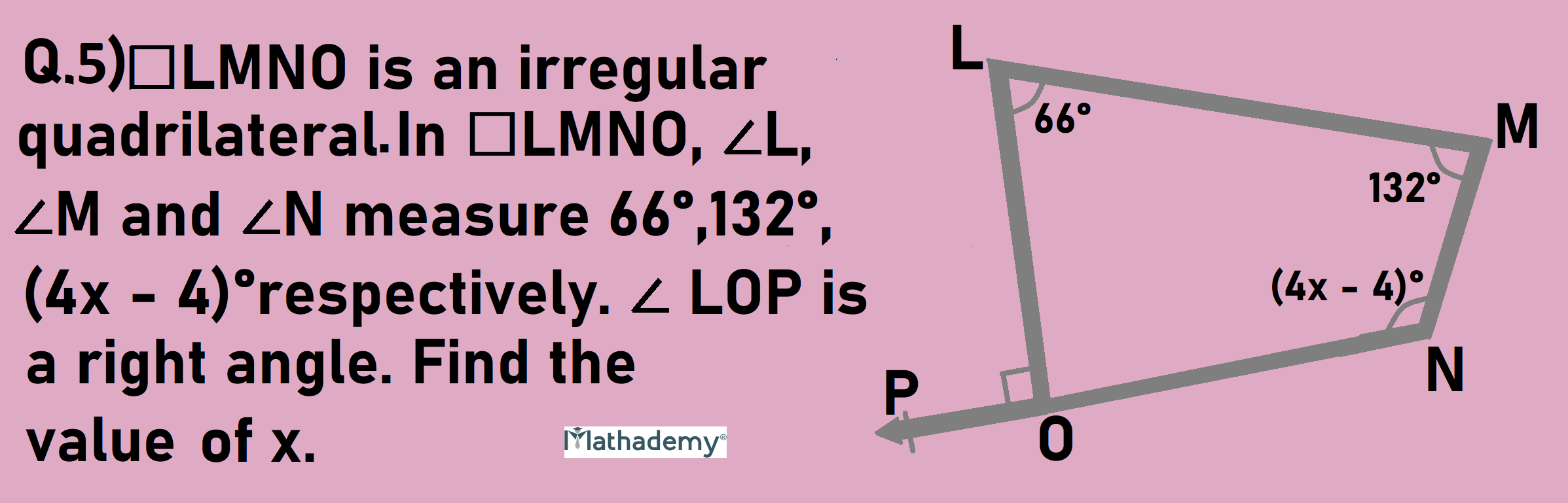
Solution:

We know that the sum of measures of ∠L, ∠M, ∠N and ∠O is 360°.

∴ ∠OLM + ∠LMN + ∠MNO + ∠NOL= 360°

∴ 66 + 132 + 4x – 4 + ∠O = 360

∴ 194 + 4x + ∠O = 360

∴∠NOL + 4x = 360 – 194

∴ ∠NOL + 4x = 166

∴ ∠NOL = 166 – 4x

We know that ∠LON and ∠LOP are in a linear pair.

∴ ∠LON + ∠LOP = 180°

∴ 166 - 4x + 90 = 180

∴ 256 – 4x = 180

∴256 - 180 = 4x

∴76 = 4x

∴76/4 = x

∴ 19 = x

Hence the value of x is 19.

Area of Quadrilaterals

Quadrilateral	Area
Parallelogram	Base * Height
Rhombus	1/2 * Length of first Diagonal * Length of second Diagonal
Rectangle	length * breadth
Square	side2
Trapezium	1/2 * sum of parallel sides * height
Kite	1/2 * length of first diagonal * length of second diagonal base * height
Irregular Quadrilateral	(1/2) * diagonal * sum of length of perpendiculars drawn to the same diagonal

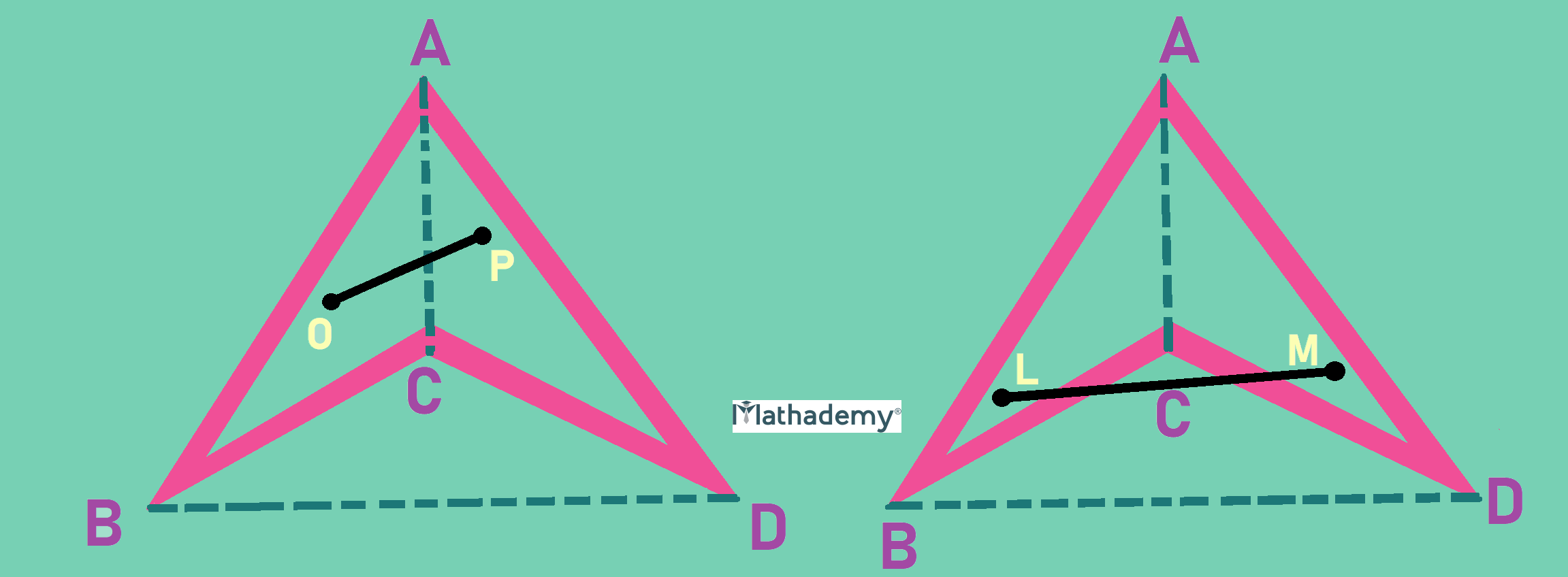
• Concave quadrilaterals

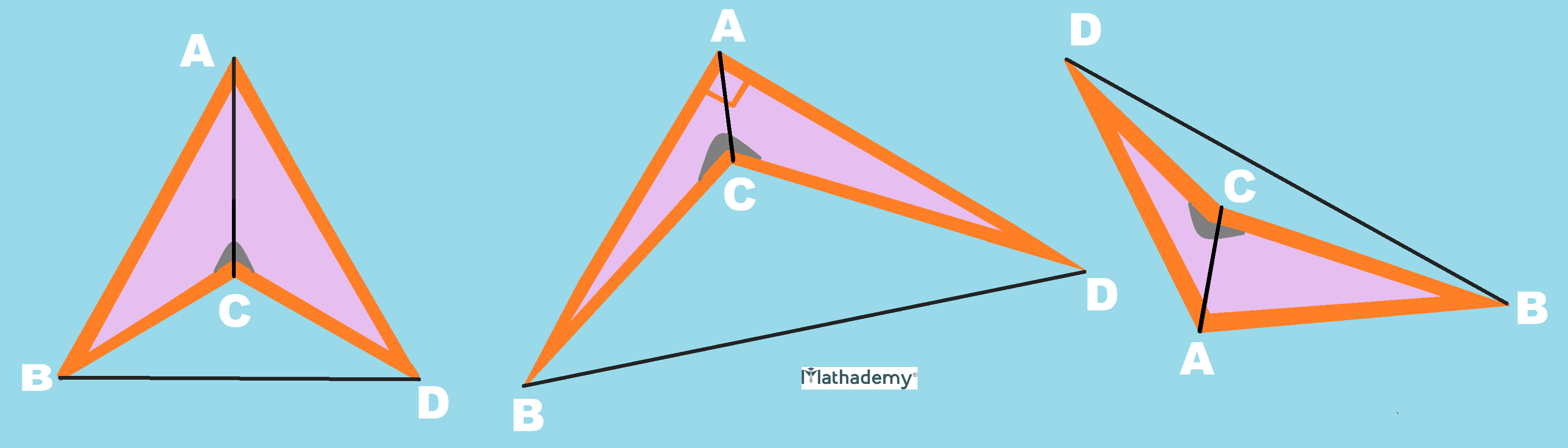
The hallmark of a concave quadrilateral is that not every segment whose endpoints are in the region enclosed by a concave quadrilateral will lie within the quadrilateral.

This is unlike convex quadrilaterals, where all the segments whose endpoints are within the interior of the quadrilateral will always lie in the area enclosed by the quadrilateral.

The figure given below evidences that. The figures above and below are of darts, which are concave quadrilaterals.

Complex Quadrilaterals

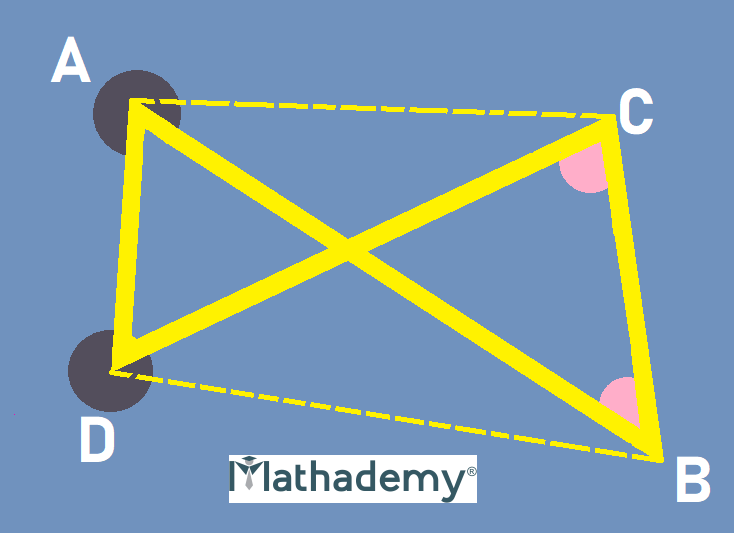
A complex quadrilateral (also known as a self intersecting/crossed/bowtie quadrilateral) is a quadrilateral in which opposite sides (only one pair) intersect. It consists of four angles, two acute interior angles and two reflex angles, which even after appearing to be exterior angles, are in fact interior angles. The sum of these four angles is always 720°, unlike simple quadrilaterals.

Though the intersection of two opposite sides seems to create two additional angles, these are not considered. The pair of acute angles and the pair of reflex angles can be on either side of the crossing.

Test your knowledge: