In Geometry, the Pythagorean theorem or Pythagoras' theorem is a statement or principle about the sides of a right triangle (A right triangle or right-angled triangle is a triangle in which one angle measures 90°). The theorem has been named after the ancient Greek thinker Pythagoras, who is credited for having discovered it.

What is Pythagoras Theorem?

The Pythagoras Theorem states that in a right triangle, the square of length of the longest side is equal to the sum of the squares of the lengths of the other two sides.

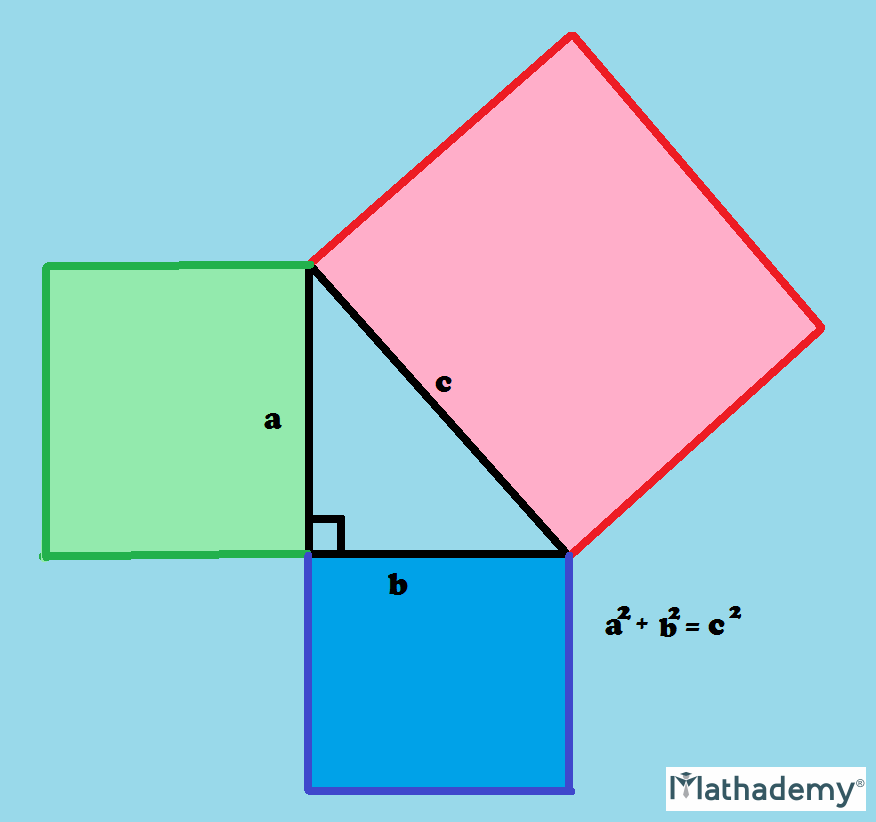
It is stated in the form of this equation: a² + b² = c².
In the above diagram, a, b and c are the sides of the triangle and c is the largest side, since it is formed by the angle of 90° right opposite to it. The longest side, c, is called as the hypotenuse and the remaining two shorter sides, which are a and b, are called as legs.
You use the Pythagorean Theorem when you know the lengths of two sides of a right triangle and you want to figure out the length of the third side.

Pythagoras Theorem Equations

• b² = c² - a² and a² = c² - b²
• c = √ (a² + b²)
• b = √ (c² - a²) and a = √ (c² - b²)

Pythagoras Theorem Formulas

The Pythagoras Theorem Formulas states that in a right angled triangle ABC, The square of the hypotenuse AC is equal to the sum of the squares of the other two sides AB and BC. It can be written as Hypotenuse² = Base² + Height² or AC² = AB² + BC².

Converse of Pythagoras theorem:

The Converse of the Pythagorean Theorem tells us that if the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

Application of Pythagoras theorem:

It is used extensively in the fields of Architecture, construction and even in navigation. The Pythagorean Theorem is greatly useful for navigation. It is one of the most useful formulas in mathematics because there are many applications of it both in the subject and in the real world. For example, architects and engineers use this formula extensively when building ramps.

Pythagoras' Theorem Example:

Q.1) John wants to convert a stairway leading from the ground to his front porch into a ramp. As visible in the figure below, the porch is 5 feet off the ground, and due to building regulations, the ramp must start 12 feet away from the base of the porch. What should be the length of the ramp that John must construct?

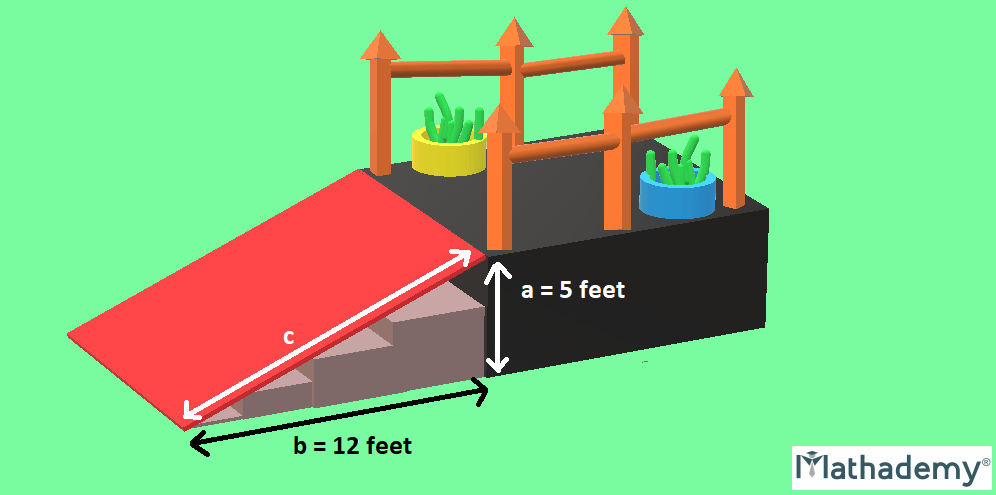
Solution: We know that a² + b² = c² (Pythagoras theorem)
∴ 5² + 12² = c²
∴ 25 + 144 = c²
∴169 = c²
∴ √169 = c
∴ ± 13 = c
Since the length of anything cannot be a negative number, the length of the ramp that John must construct is 13 feet.

Pythagorean Triples:

In mathematics, a Pythagorean triple is called as a set or group of three positive integers which satisfy the equation a² + b² = c², we call such numbers triples or triplets. The most well-known examples of such triples are (3,4,5) and (5,12,13). When we multiply the numbers in a triple, e.g. (3,4,5) by 2, we get another triple : (6,8,10). (9,12,15) and (15,20,25), (7, 24, 25), (8, 15, 17), (9,40,41), (11,60,61), (12,35, 37), (16, 63, 65), (20, 21, 29) are a few other examples of triplets..

Pythagoras' Theorem Example:

Q.2) In the figure below, a ladder that measures 10 m in length is placed on the ground in such a way that it touches the top of a vertical wall 8 m high. Find the distance from the foot of the ladder to the bottom of the wall.

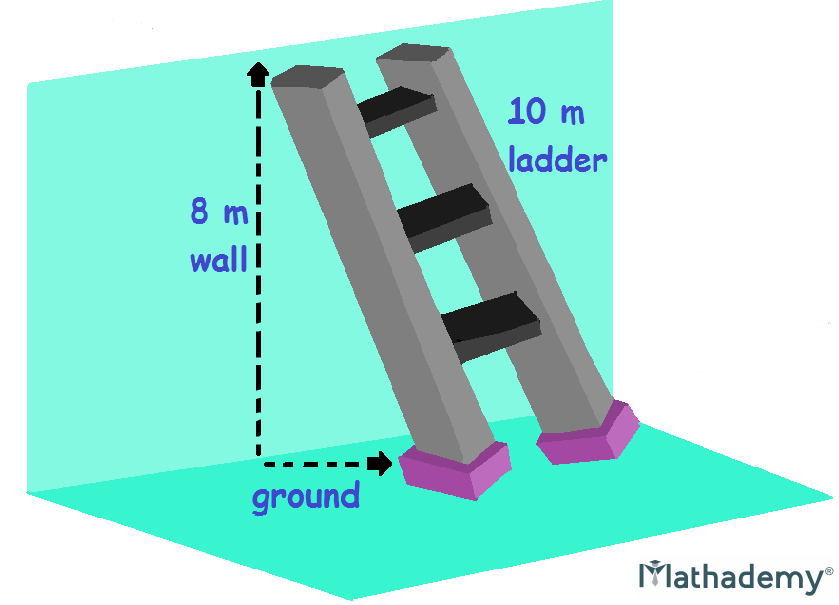
Solution: Let the required distance be x meters. Here, the ladder, along with the wall and the ground form a right-angled triangle. The ladder will be the hypotenuse of that triangle, since the wall and the ground make an angle of 90°.
We know that according to Pythagoras’ Theorem,
x² + 8² = 10²
∴ x² = 10² – 8²
∴ x² = 100 – 64
∴ x² = 36
∴ x = √36
∴ x = ± 6
Since distance cannot be negative, the distance between the foot of the ladder and the wall is 6 m.

Pythagoras' Theorem Example:

Q.3) Heights of two buildings AB and CD are 49 m and 25 m respectively. If the distance between the two buildings is 7 m, then find the distance between their tops.

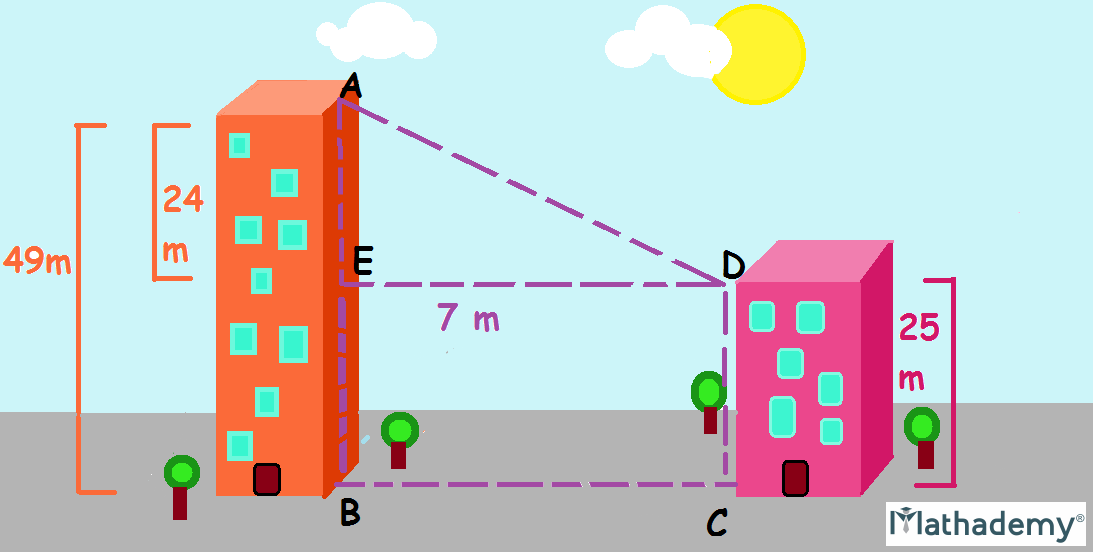
Solution: We know that the heights of vertical buildings AB and CD are 49 m and 25 m, respectively.
When we draw DE perpendicular (forming an angle of 90°) at a point E on AB,
Then AE = AB – EB and EB = DC = 25 m (The buildings stand parallel to each other)
∴ AE = 49 m - 25 m = 24 m
Now, AED is right angled triangle and right angled at E.
∴ AD² = AE² + ED²
∴AD² = 24² + 7²
∴ AD² = 576 + 49
∴ AD² = 625
∴ AD = √625
∴ AD = ± 25
Since the distance between the buildings' tops cannot be negative, the distance is = 25 m.

Test your knowledge: