The prime reason behind studying mathematics is to be able to count and to be able to arrive at answers. To do this, we simply use certain counting techniques. The branch of mathematics concerned with the various methods of counting is known as Combinatorics. Permutation and combination employ these techniques and spare us the effort of manually enumerating the desired outcomes one by one. These concepts not only help us tell apart one set of things from another, but also make us grasp how the items of any single group can be arranged in numerous patterns amongst themselves.

Fundamental principle of counting:

Rule of product:

If a certain action can be performed in ‘a’ number of ways and another, in ‘b’ number of ways, then both these actions can be done in a x b number of ways.

Note that the rule of product can be extended to more than two factors as well. Let us see an example where there are 3 factors.
In the aerial view of the town given below, the green dot on the left-hand side marks the entry of the town. Then, we have a path to a row of 3 cafes, C1, C2 and C3. The path from the cafes leads to a row of 2 banks, B1 and B2. From the row of the 2 banks originates a common path to the final row of library buildings, L1 and L2. Finally, the roads from the libraries converge into a path with the red dot on it, marking the end of the town.

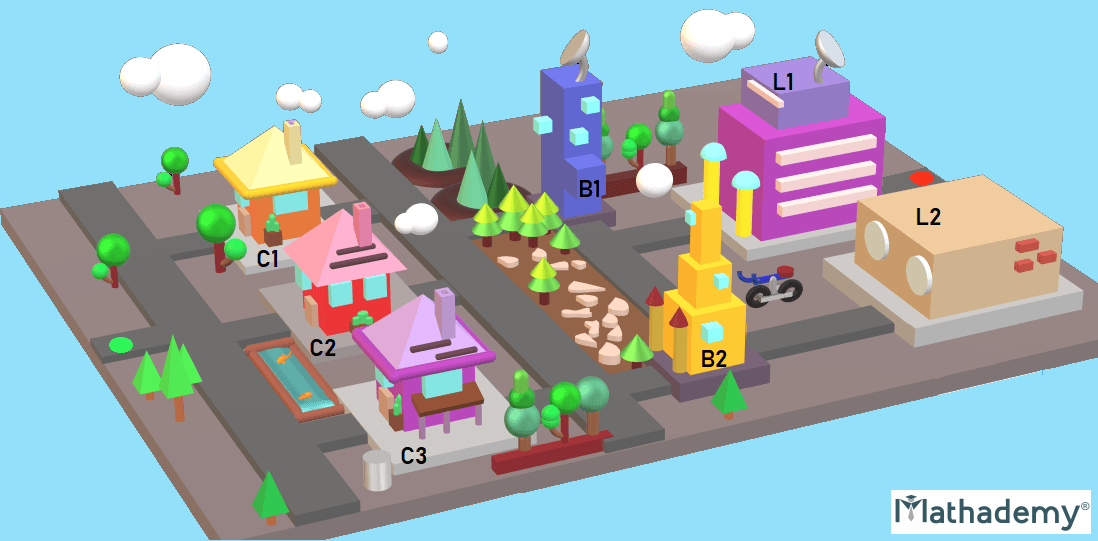
To find the ways to cross this town and get to its end, you could manually start counting and framing routes randomly. For example, one could enter the town, go to café C1, then to bank B1, and then go through library L1 and exit the town. This approach is laborious and time consuming. Although the number is finite, it will take you a while to figure out the total number of ways in which it can be accomplished.

Note that the whole deal will occur in stages, the first task being the selection of 1 of the 3 cafes, the second being the selection of 1 of the 2 banks and the third being the selection of 1 of the 2 libraries.
1. There are 3 options for the cafes
2. There are 2 options for the banks
3. There are 2 options for the libraries
∴ According to the rule of product, the number of possible ways to cross the town = 3 X 2 X 2 = 12 ways

Rule of sum:

If there are ‘m’ number of choices or ways for doing something and ‘n’ number of choices or ways for doing another thing and they cannot be done together at the same time, then there are m + n ways of doing one of all those things.

Note that the rule of sum can be extended to more than two factors as well. Let us see an example where there are two factors.
Given below are the dishes at two stores, A and B. Store A sells French fries, pizza and burger while store B sells waffle and cake. When we are to buy a single dish from either of the stores, we apply the rule of sum and figure out the total number of ways in which we can do it. We can either buy 1 of the 3 dishes from store A or 1 of the 2 dishes from store B.
There are 3 options for store A in case we chose it or there are 2 options for store B in case we chose it.
∴ According to the rule of sum, the number of possible ways in which only a dish can be chosen and bought = 3 + 2 = 5 ways

OR

Factorial:

The factorial of any positive integer is obtained by multiplying every positive integer lesser than the concerned number to it. The factorial function is denoted by an exclamation mark.

For instance, 7 factorial is denoted as 7! and its mathematical value is 7 x 6 x 5 x 4 x 3 x 2 x 1 = 5040.
It is vital that we know the factorial function since combinatorics heavily relies on it. The factorial function exists for non-negative integers only.

n! = n (n-1)! = n x (n – 1) x (n – 2 ) x (n - 3)… 2 x 1

By rule:
1! = 0! = 1
Let’s understand why 0! = 1
We know n! = n (n-1)!
Let n=1
Then we get 1! = 1(1-1)!
1! = 1*0!
1 = 0!
Since not selecting an item or element (which ideally can be represented in numerical terms as 0!) is also a formal choice, 0! = 1. The 1 stands for the choice of not selecting anything.

Permutation

When all or some of the elements of a given collection of items are arranged in a definite arrangement or an order, or when the already existing arrangement of the same objects is rearranged into different orders, various permutations are created. In other words, in a permutation, the sequence or the choices of the objects does matter and makes all the difference.

Since permutations concern themselves with pattern and order so greatly, they are of paramount importance in our real life. For instance, if the passcode of our phone is 1234, it is vital we enter that and that alone since our phone won’t accept any other permutations like 3421, 1243 etc. The words in the English language ultimately are permutations of alphabets and deviating from any word’s deemed order would either change its meaning entirely or create a meaningless word. For instance, both the words, ‘care’ and ‘race’ have been made using the same letters but have different meanings entirely, again because they are two different permutations of the same four letters a, c, e and r.

Permutation Formulas

1. Permutations of n distinct items all taken at a time = n!

Let us study a case where 4 different elements have to be arranged amongst themselves in a row. We begin to find out the number of permutations by denoting the four places by dashes.
Since 1 of the 4 distinct elements can be in the first place, the first place has 4 choices:
4 x __ x __ x __
Since 1 of the 4 distinct elements is already placed, the second place has 3 choices remaining:
4 x 3 x __ x __
Since the first two of the elements have already been placed, the third place has 2 choices remaining:
4 x 3 x 2 x __
Since the first three of the elements have already been placed, the last place will naturally have 1 choice remaining:
4 x 3 x 2 x 1 = 4! = n! (n = 4)
Hence, permutations of 4 distinct items all taken at a time = 4! = 24

Permutation Example:

Q.1) In the above diagram, there are 3 cones of ice cream. In how many ways can those 3 different sorts of ice cream, namely strawberry, mango and guava be distributed amongst 3 friends, X, Y and Z if all 3 friends like different cones?

Solution: We must distribute all 3 different sorts of ice cream amongst 3 people and everyone must have a different cone.
∴ The number of ways in which those 3 types of ice cream can be distributed amongst 3 people = 3! = 3 x 2 x 1 = 6

Hence, in 6 different ways can the distribution of those 3 different cones be done amongst 3 people.

2. Permutations of n distinct items taken r at a time (repetition not allowed) = P(n,r) = ⁿP_r = n!/(n-r)!

Let us study a case where 2 out of 4 different elements have to be arranged amongst themselves. We begin to find out the number of permutations by denoting the two places by dashes, since we have to arrange only two and not all four of the given objects.
Since 1 of the 4 distinct elements can be in the first place, the first place has 4 choices:
4 x __
Since 1 of the 4 distinct elements is already placed, the second and the final place will have 3 choices remaining.
4 x 3 = 12
Now let’s verify this with the formula, here n = 4 and r = 2
ⁿP_r = n!/(n-r)! = 4!/(4 – 2)! = 4!/2! = (4 x 3 x 2!)/2! = 4 x 3 = 12
Hence, permutations of 4 distinct items taken 2 at a time (repetition not allowed) = 4 x 3 = 12

Permutation Example:

Q.2) In the above diagram, there are five different drinks. In how many ways can these 5 drinks be served to 2 customers if both cannot be given the same drink?

Solution: We know that we cannot serve the same two drinks to the 2 customers.
∴ The number of way in which those 2 customers can be served 5 drinks = ⁵P₂
= 5!/(5 – 2)!
= 5!/3!
=5 x 4 x 3!/3!
= 5 x 4
= 20
Hence, the 5 drinks can be served to 2 customers in 20 different ways.

3. Permutations of n distinct items taken r at a time (repetition allowed) = n^r

Let us study a case of making permutations of any 2 of the 4 elements, where the repetition of elements is allowed. The permutations have to be made considering the fact that the elements can be repeated and that the number of choices will not reduce after placing any of the available elements since all of the elements can be used more than just once.
Since 1 of the 4 distinct elements can be in the first place, the first place has 4 choices:
4 x __
Since any of the elements placed first can be repeated the second time, the second place will have again have four choices:
4 x 4 = n x n = n² = n^r (n = 4, r = 2)
Hence, permutations of 4 distinct items taken 2 at a time (repetition allowed) = 4 x 4 = 16

Permutation Example:

Q.3) Edna wants to buy a bouquet of 3 flowers. Each flower is available in 3 colours, red, yellow and blue. In how many ways can the bouquet of those 3 colours be bought?

Solution: We know that every flower is available in 3 colours.
Since the colours of the flowers can be repeated, the number of ways in which Edna can buy those 3 flowers’ bouquet = 3³
= 3 x 3 x 3 (∵ there are 3 choices for every flower and there are a total of 3 flowers)
= 27
Hence, the number of ways in which the flower bouquet can be bought is 27.

4. Permutations of n items of which p items are of one kind and alike, q are of a second kind and alike and r are of a third kind and alike = n!/p!q!r!

Let us study the case of the word ‘GOGGLES’, which is made up of the letters G, O, L, E and S, of which Gs are 3 of one sort and alike and the remaining letters O, L, E and S exist individually.
Let us temporarily name the Gs as G1, G2 and G3 and treat them as 3 separate letters or entities. By that modification, we have the letters G1, G2, G3, O, L, E and S occurring individually. The total number of permutations of these 7 distinct letters without repetition would be 7! . When we consider the distinct letters G1, G2 and G3, the number of ways in which these 3 distinct letters would be arranged amongst themselves is 3! = 6 ways:
G1, G2, G3
G1, G3, G2
G2, G1, G3
G2, G3, G1
G3, G1, G2
G3, G2, G1
These permutations are a part of the total permutations of the 7 lettered parent word in the form of 3! . Simply said, 7! (the arrangements of the total 7 letters) is inclusive of 3! (the arrangements of the 3 distinct Gs, which are G1,G2, and G3)
However, when we consider the original word ‘GOGGLES’, we realise that the letter G is simply repeated thrice and no matter how one arranges the three Gs, one would get only 1 permutation of theirs or only 1 way to arrange them: G, G, G
Hence, to find out the true number of permutations of the original word ‘GOGGLES’, we simply take the factorial of the number of elements present in the word and then divide it by the factorial of the repeating elements:
7!/3! = 7 x 6 x 5 x 4 x 3!/3! = 7 x 6 x 5 x 4 = 840 = n!/p! (n = 7, p = 3)
This ensures getting rid of the extra arrangements and retains only that one permutation, which in this case is G, G, G.
Hence, permutations of 7 items of which 3 items are of one kind and alike = 840

Permutation Example:

Q.4) In how many ways can the permutations of the word ‘keenness’ be made?

Solution: We know that the word ‘keenness’ contains 8 letters of which e is repeated thrice, n, s are repeated twice and k appears just once.
∴ The number of permutations of the letters of the word ‘keenness’ = 8!/3!2!2!
= 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1/ 3 x 2 x 2 x 2
= 1680
Hence the letters of the word ‘keenness’ can be arranged in 1680 ways.

Combination

When a certain number of things are selected from a collection of distinct/individual things or items by not taking into consideration the order in which they are chosen, a combination is created. In other words, in a combination, the sequence of the choices does not matter or does not make a difference.

For instance, in case of selecting 3 sorts of fruits out of a total of 4 fruits available – strawberry, mango, guava and apple, the combinations can be come up with making a group of 3 selected sorts at a time:
1) apple + mango + guava [rejecting strawberry]
2) apple + strawberry + guava [rejecting mango]
3) apple + strawberry + mango [rejecting guava]
4) strawberry + mango + guava [rejecting apple]
It is also done by simply rejecting 1 fruit at a time and we would be left with 4 combinations of the remaining 3 fruits by default. Thus, in either case, we get the 4 combinations listed above.

After you’ve your heart set on any of these 3 fruits’ choice, the sequence of the purchase will not make a difference. What, however, does matter is that you stick to the same fruits. That is the essence of a combination. In a combination, the position or order of the elements does not matter. Words like ‘set’ and ‘group’ are synonymous with the word ‘combination’.

Combination Formula

5. Combinations of n items taken r at a time (without repetition) = C(n, r) = ⁿC_r = ⁿC_n-r = n!/r!(n –r)!

Let us take the case of selecting 2 items from a total of 4 items, A, B, C and D, without repetition. Before we dive into the ways of selecting those two items, let us first find out the number of permutations of any 2 items chosen from the total 4 items. We know that the permutations of 4 distinct items taken 2 at a time (repetition not allowed) = ⁴P₂ = 4!/(4 –2)! = 4!/2! = 4 x 3 = 12
Let us take two of the total twelve permutations and study them. For instance, one permutation is AB and another is BA. Note that these permutations are made up of the same two elements, A and B. We can conclude that even other ten permutations must consist of such pairs. Any two separate elements can be arranged in 2! = 2 ways. Ideally, for every two elements, there is one combination. In other words, 2! permutations are there for a 1 combination. Hence for 12 permutations, the combinations will be:
12/2! = 6
Now let’s verify this with the formula, here n = 4 and r = 2
n!/r!(n –r)! = 4!/(2!)(4-2)! = 4!/(2!2!) = 6
By simple cross multiplication, if there is 1 combination for 2! or 2 permutations, there will be 6 combinations for 12 permutations.
Hence combinations of 4 items taken 2 at a time (without repetition) = 6

Combination Example:

Q.5) There is a group of 5 boys and 4 girls in a school. A team of four people must be formed in which there is an equal number of boys and girls. In how many ways can this be done?

Solution: We must have an equal number of boys and girls in the team of 4 members.
∴ We must select 2 boys from the total 5 boys and 2 girls from the total 4 girls.
Since the boys can be chosen in ⁵C₂ ways and the girls can be chosen in ⁵C₂ ways, the number of ways in which the team can be made = ⁵C₂ x ⁴C₂ = 5! x 4! / 2!(5-2)! 2!(4-2)!
= 5! x 4! / 2!3! x 2!2!
= 5 x 4 x 3! x 4 x 3 x 2! / 2 x 3! x 2! x 2!
= 5 x 4 x 4 x 3 / 2! x 2!
= 5 x 4 x 3
= 60
Hence, the number of ways in which the team members can be selected is 60.

Test your knowledge: