In basic mathematics, HCF and LCM play a rather crucial role in the operations involving both multiplication and division. Let us have a closer look at the concepts on which the entire ideas of HCF and LCM have been founded.

What is HCF and LCM?

Say that your friend has baked you a delicious chocolate cake. On enquiring about what makes it so perfect, he tells you the secret lies in the ratio of the cocoa powder to the flour, and that he’s put in 48 grams of the powder and 72 grams of flour. Therefore, the ratio of the cocoa powder to the flour becomes 48 : 72.
When we want to simplify this by reducing the ratio to its smallest terms, the role of HCF comes in. We arrive at the highest common factor or divisor of both 48 and 72 and divide them into the smallest terms.
Since the HCF of 48 and 72 is 24, 48/72 = 24*2/24*3 = 2/3
Hence, we now have the ratio of the cocoa powder and the flour as 2 : 3 .

Say on Diwali, an orange light flashes every 6 seconds and another green one, every 18 seconds. They’re turned on at the same time at 7 P.M and we must figure out the time they’ll flash together next. This is where the role of LCM comes in. When the orange light will have flashed after being turned on, the green one will not have. However, 6 seconds will have gone by. When the orange light will have flashed the second time, 12 seconds will have gone by. The green light will not have flashed even yet. Finally, when the orange light will have flashed for the third time, 18 seconds will have gone by and this time, the green one will have flashed too. Hence, they both will flash together for the first time after being turned on 18 seconds after 7 P.M. Thus, LCM is useful in finding out when two things having different frequencies will occur together next.

In order to understand HCF (Highest common factor) and LCM (Least Common multiple), we first need to get an idea about factors and multiples.

When we talk about the factor of any number, we refer to any number that divides the number completely, with no remainder. For instance, the factors of 27 are: 1, 3, 9 and 27 itself. The number 10 cannot be divided by 4 without a remainder. When we divide 10 by 4, we get the answer as 2.5, which is not an integer. That is why, 4 cannot be termed as a factor of 10. We must remember that factors are always lesser than or equal to the original number.

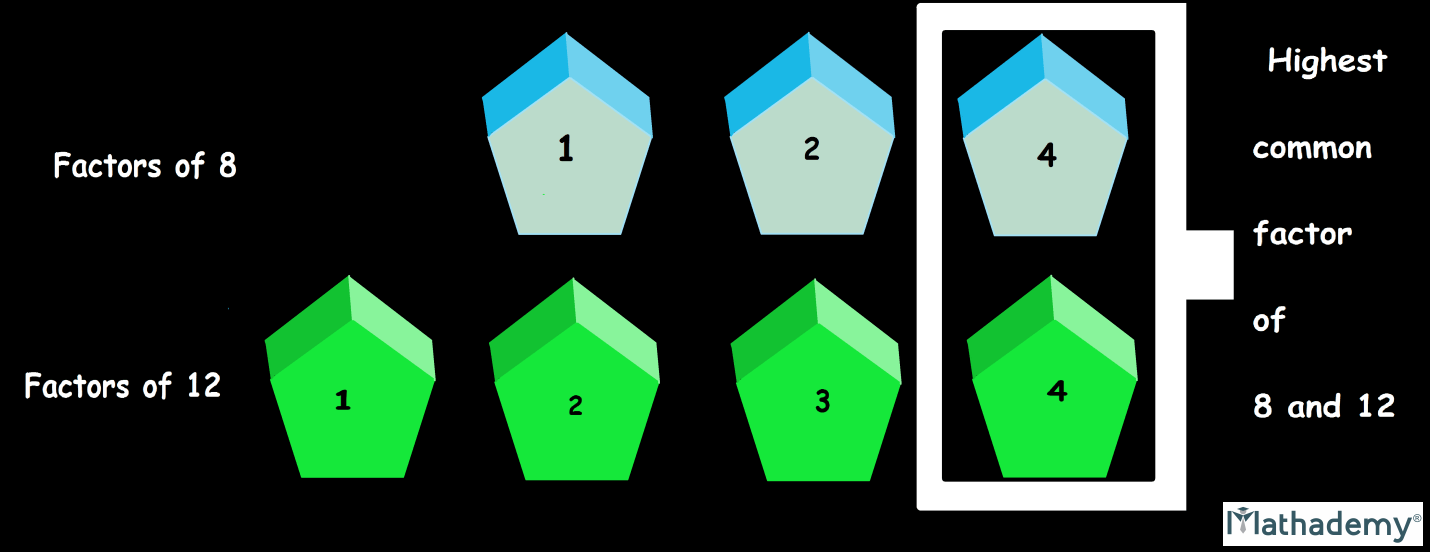
On the other hand, when we talk about multiples, when you learned your times tables in primary school, you were learning multiples. For examples, 2, 4, 6, 8, and 10, 12 are all multiples of 2. In order for us to obtain these numbers, you multiplied 2 by 1, 2, 3, 4, 5 and 6, which are integers. A multiple of a number is that number multiplied by an integer.

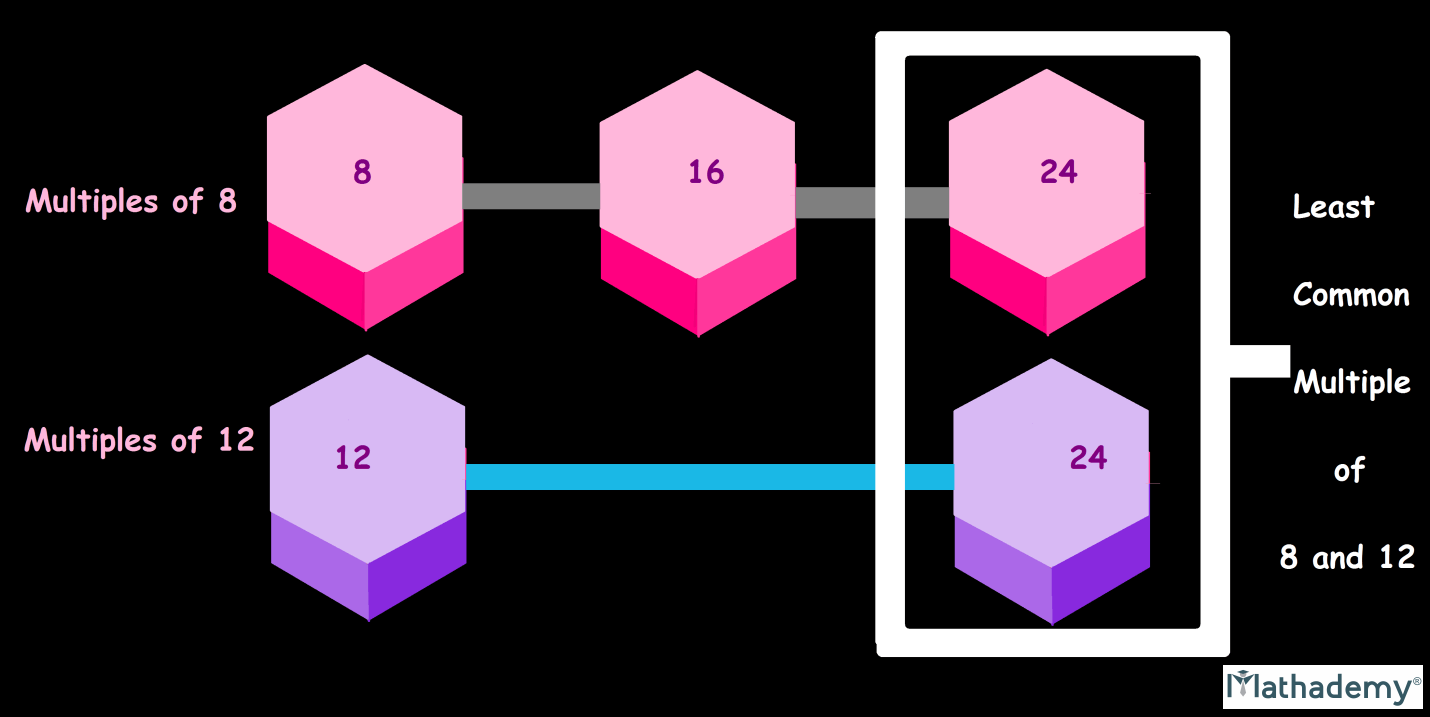
Now that we’ve gained clarity on what multiples and factors are, we’ll proceed towards the formal definition of HCF and LCM and understand them even better.

• Highest Common Factor (HCF):

The largest or greatest factor common to any two or more than two given natural numbers is called as HCF of the respective numbers. Remember that it is also known as GCD (Greatest Common Divisor). For instance, HCF of 4, 6 and 8 is 2.

• Lowest Common Multiple (LCM):

It refers to the least or smallest common multiple of any two or more than two given natural numbers. For instance, LCM of 10, 15, and 20 is 60.

Methods to find out the HCF of two or more given numbers:

•HCF by Factorization Method:

In this method, we write down all the factors/divisors of the concerned two or more than two numbers. After listing down the divisors of the said numbers, we take notice of the greatest or the highest number that commonly divides the numbers without leaving any remainder. That number is said to be the numbers’ Highest Common Factor or Greatest Common Divisor.

HCF and LCM Example:

Q.1) Find the HCF of 36 and 45 using the factorization method.
Solution: We know that the factors of 36 are 1, 2, 3, 4, 6, 9, 12, 18 and 36 itself. (1 × 36, 2 × 18, 3 × 12, 4 × 9, 6 × 6)
We know that the factors of 45 are 1, 3, 5, 9, 15 and 45 itself. (1 × 45, 3 × 15, 5 × 9)
As we can conclude, the highest or the greatest factor in terms of value of both 36 and 45 is 9, the HCF of 36 and 45 is 9.

• HCF by Prime factorization method:

In this method, we write down the two or more numbers as products of prime factors. We then identify the prime factors that are common to the concerned numbers. These common prime factors’ product is said to be the numbers’ Highest Common Factor or Greatest Common Divisor.

HCF and LCM Example:

Q.2) Find the HCF of 36 and 48, using prime factorization method.
Solution: We first find out the prime factors individually.

Methods to find out the LCM of two or more given numbers:

•LCM by Prime factorization:

In this method, we write down the two or more numbers as products of prime factors. We then identify the prime factors that are common to the concerned numbers. When we multiply the product of these common factors to the uncommon factors present in the concerned numbers, we get the Least Common Multiple.

HCF and LCM Example:

Q.3) Find the LCM of 8 and 24 using prime factorization.
Solution: We first find the prime factors of the numbers 8 and 24.

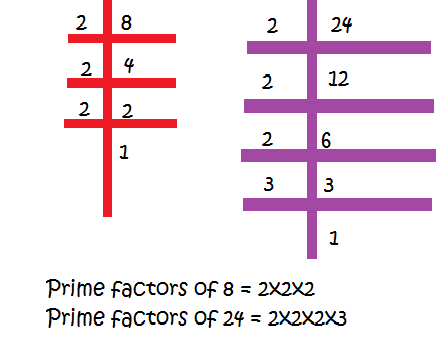
We see that the common factors of 8 and 24 are 2 x 2 x 2 and the uncommon factor is 3. The LCM of 8 and 24, hence, is 2 x 2 x 2 x 3.
The product of these numbers is 24. So the LCM of 8 and 24 is 24.

•LCM by Division method:

We first write all the given numbers in a single row, separated by commas. Secondly, we find the least prime number that divides at least two numbers from the set of given numbers. We then write the quotients exactly below the respective number. The numbers which are not divisible by that prime number must be written as they are, below the respective number. We keep repeating the second step until no two numbers are divisible by the same number. To obtain the LCM, we multiply the divisors and remaining quotients and the product of all these is the LCM of the given set of numbers.

HCF and LCM Example:

Q.4) Applying the division method, find the LCM of 15, 30 and 90.
Solution:

Now we find the product of divisors and the remaining quotient. For the given numbers 15, 30 and 90 the product of divisors and quotients or the LCM = 2×3×5×3 = 90.

HCF and LCM Formula:

• The product of LCM and HCF of any two respective natural numbers is equal to the product of the given numbers.
LCM × HCF = Product of the numbers (applicable for two numbers)
Suppose X and Y are two numbers, then LCM (X and Y) × HCF (X and Y) = X × Y
• When two numbers (they may not be prime) do not have any common factor other than one between them, they are called co-prime or relatively prime. HCF of co-prime numbers is 1. Therefore LCM of given co-prime numbers is equal to the product of the numbers.

LCM of co-prime numbers = Product of the numbers

HCF and LCM Example:

Q.5) X, Y start to jog around a circular stadium in the same direction. They complete their rounds in 9 seconds, 8 seconds respectively. After how many seconds will they be together at the starting point?
Solution: Every time X completes a round, he takes 9 additional seconds. Every time Y completes a round, he takes 8 additional seconds. When we continue further, we see that both the multiples meet at 72.

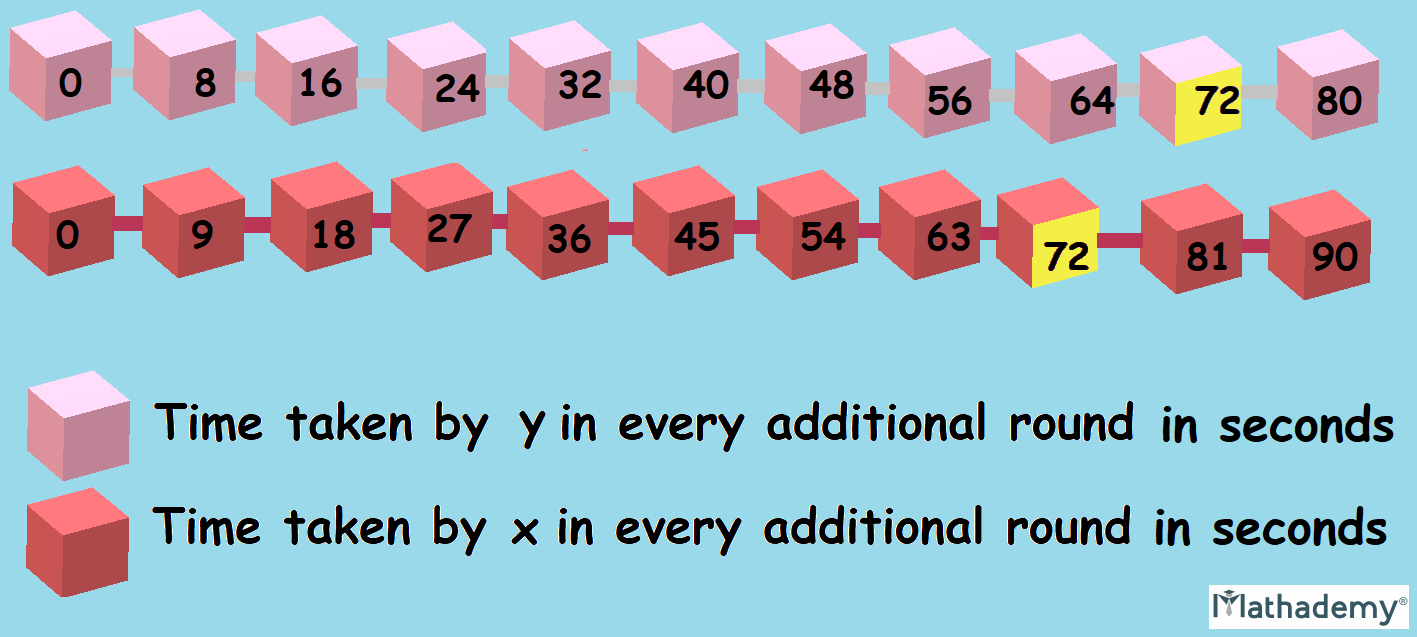
We know that the required time is the LCM of all their lap times. This is the earliest when both will intersect at the same point.
Required time is the LCM (9, 8) which is 72.
∴ the required time is 72 seconds.

HCF and LCM of Fractions

LCM of fractions = LCM of numerators / HCF of denominators
HCF of fractions = HCF of numerators / LCM of denominators

Test your knowledge: